Problème de Monty Hall

Le nom de ce problème mathématique vient du nom de l’animateur d’origine canadienne Monty Hall qui a présenté ce jeu aux États-Unis pendant treize ans. Voici son déroulement :

Le jeu oppose un présentateur à un candidat (le joueur). Ce joueur est placé devant trois portes fermées. Derrière l’une d’elles se trouve une voiture et derrière chacune des deux autres se trouve une chèvre. Il doit tout d’abord désigner une porte. Puis le présentateur ouvre une porte qui n’est ni celle choisie par le candidat, ni celle cachant la voiture (le présentateur sait quelle est la bonne porte dès le début). Le candidat a alors le droit ou bien d’ouvrir la porte qu’il a choisie initialement, ou bien d’ouvrir la troisième porte.

La question que l’on se pose est :
Quelle est la stratégie qui offre le plus de chance de gagner la voiture ?

La fonction suivante permet de simuler une partie de ce jeu. Si le paramètre vaut "change" le joueur change de porte, sinon, il conserve son choix initial. Cette fonction renvoie le gain obtenu.

def MontyHall(change_porte):
  # simule une partie du jeu de Monty Hall

  # choisir la porte de la voiture
  porte_voiture=randint(1,3)

  # le joueur choisit une porte au hasard
  choix1=randint(1,3)

  # Monty Hall ouvre une porte montrant une chèvre
  # construire la liste des portes pouvant être ouvertes
  nb_portes=0
  liste_portes=[]
  for i in range(1,4):
    if i<>porte_voiture and i<>choix1:
      liste_portes.append(i)
      nb_portes=nb_portes+1
            
  # choisir au hasard une porte à ouvrir parmi celles possibles
  choix_Monty = liste_portes[randint(0,nb_portes-1)]
  # construire la liste des portes restantes pour le joueur
  liste_portes = []
  for i in range(1,4):
    if i<>choix_Monty:
      liste_portes.append(i)
            
  # le joueur choisit une porte à ouvrir
  if change_porte=="change":
    if liste_portes[0]==choix1:
      choix2=liste_portes[1]
    else:
      choix2=liste_portes[0]
  else:
    choix2=choix1
        
  # on regarde ce que le joueur gagne
  if choix2==porte_voiture:
    return("Voiture")
  else:
    return("Chevre")

Une fois compilée, on crée un tableau qui simule dans une colonne 100 parties de ce jeu en faisant changer le joueur de porte. Dans une autre colonne on simule 100 autres parties en ne faisant pas changer le joueur de porte. On calcule la fréquence de gain de la voiture dans chaque cas :

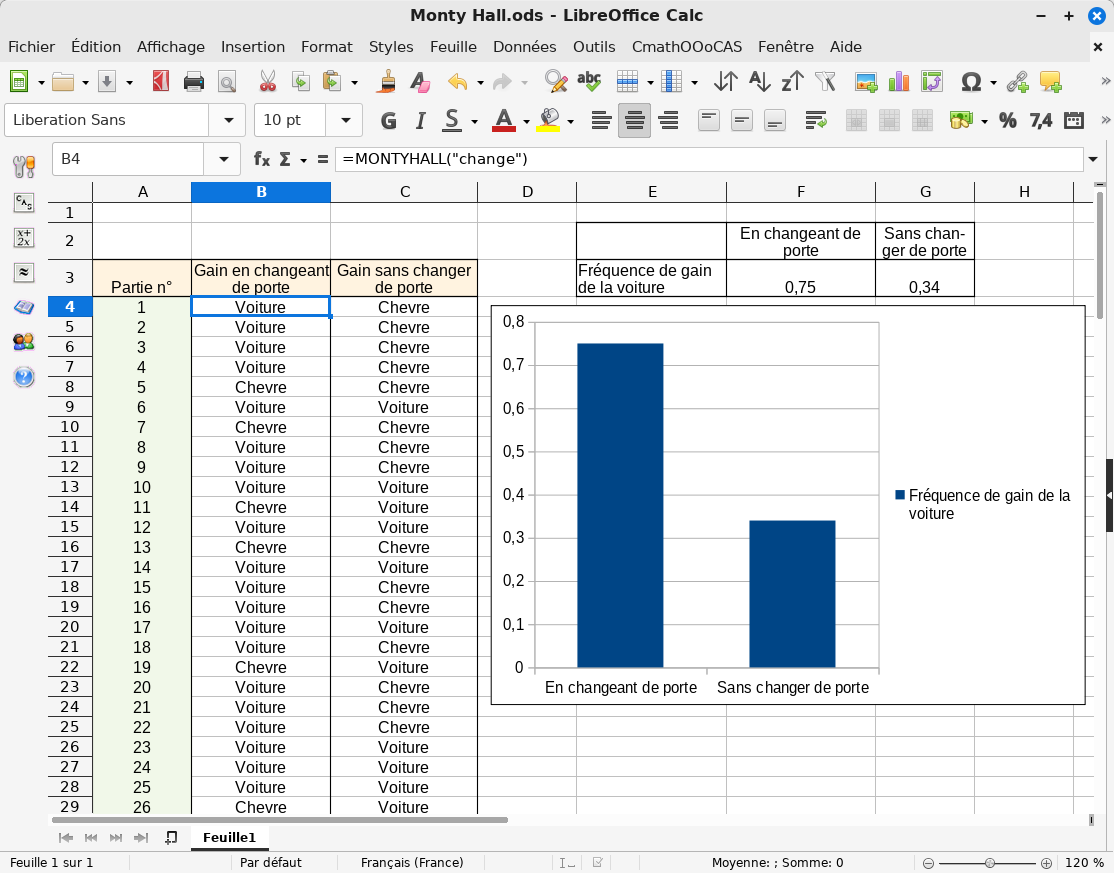
En appuyant sur Ctrl+Maj+F9, Calc recalcule toutes les cellules ce qui permet de resimuler 200 nouvelles parties. On constate qu’il vaut mieux changer de porte pour espérer gagner la voiture.